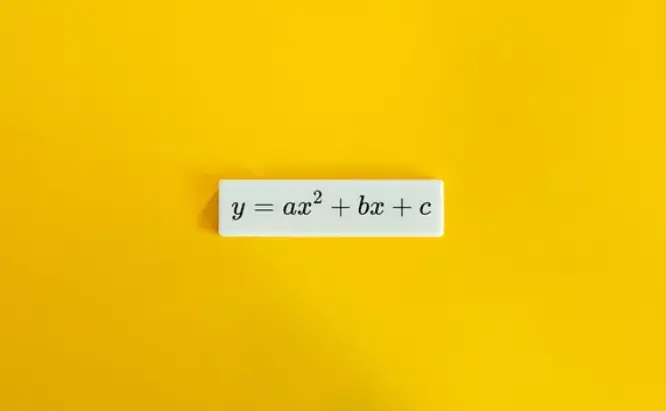A equação do 2º grau, também chamada de equação quadrática, é uma das mais importantes ferramentas matemáticas no ensino básico e na vida prática. Neste artigo, vamos explorar como resolver uma equação do 2º grau, identificar seus componentes e oferecer exemplos e exercícios para consolidar o aprendizado.

O que é uma equação do 2º grau?

Uma equação do 2º grau é uma equação polinomial cujo maior expoente da incógnita é igual a dois. Ela possui a forma geral:

Nesta equação:

• \\( x \\) é a incógnita, ou seja, o valor desconhecido a ser determinado.
• \\( a \\), \\( b \\) e \\( c \\) são chamados de coeficientes.
• O coeficiente \\( a \\) deve ser diferente de zero, caso contrário, a equação se transforma em uma equação do 1º grau.

Resolver uma equação do 2º grau significa encontrar os valores de \\( x \\) que tornam a equação verdadeira, conhecidos como as raízes da equação.

Tipos de Equações do 2º Grau

As equações do 2º grau podem ser classificadas em completas ou incompletas:

• Equação completa: Todos os coeficientes \\( a \\), \\( b \\) e \\( c \\) são diferentes de zero.
  Exemplo:
• Equação incompleta: Um ou mais coeficientes podem ser iguais a zero.
  Exemplos:
  • \\( b = 0 \\):
  • \\( c = 0 \\):
  • \\( b = 0 \\) e \\( c = 0 \\):

Exemplo 1 — Equação incompleta com \\( b = 0 \\)

Determine os valores de \\( x \\) que tornam a equação:

verdadeira.

Solução:

Essa é uma equação incompleta com \\( b = 0 \\). Para resolver, isolamos o \\( x \\):

Portanto, as raízes são \\( x = -2 \\) e \\( x = 2 \\).

Fórmula de Bhaskara

Quando lidamos com equações completas, a fórmula mais utilizada para encontrar as raízes é a fórmula de Bhaskara. Ela se baseia no cálculo do discriminante \\( \\Delta \\), que nos dá informações sobre o número de raízes reais que a equação possui.

A fórmula de Bhaskara é:

O discriminante \\( \\Delta \\) é dado por:

Como resolver uma equação do 2º grau usando Bhaskara?

Passo 1: Identificar os coeficientes \\( a \\), \\( b \\) e \\( c \\). Por exemplo, para a equação:

temos:

• \\( a = 2 \\)
• \\( b = -3 \\)
• \\( c = -5 \\)

Passo 2: Calcular o discriminante \\( \\Delta \\). Substituímos os valores de \\( a \\), \\( b \\) e \\( c \\) na fórmula do discriminante:

Passo 3: Calcular as raízes. Agora que temos \\( \\Delta = 49 \\), substituímos na fórmula de Bhaskara:

Temos duas soluções:

As raízes da equação \\( 2x^2 – 3x – 5 = 0 \\) são \\( x = 2,5 \\) e \\( x = -1 \\).

Analisando o discriminante

O valor de \\( \\Delta \\) nos permite determinar quantas e quais são as raízes de uma equação do 2º grau:

• Se \\( \\Delta > 0 \\), a equação tem duas raízes reais e distintas.
• Se \\( \\Delta = 0 \\), a equação tem uma raiz real dupla.
• Se \\( \\Delta < 0 \\), a equação não possui raízes reais.

Exemplo 2 — Equação incompleta com \\( c = 0 \\)

Encontre as raízes da equação:

Solução:

Essa é uma equação incompleta com \\( c = 0 \\). Podemos fatorar a equação:

Para que o produto seja zero, temos duas soluções possíveis:

Portanto, as raízes são \\( x = 0 \\) e \\( x = 3 \\).

Exercícios Propostos

Questão 1: Resolva a equação:

utilizando a fórmula de Bhaskara.

Solução:

Identificando os coeficientes:

• \\( a = 2 \\)
• \\( b = 7 \\)
• \\( c = 5 \\)

Calculando o discriminante:

Agora, usando a fórmula de Bhaskara:

As soluções são:

As raízes são \\( x = -1 \\) e \\( x = -2,5 \\).

Questão 2: Resolva a equação incompleta:

Solução:

Fatoramos a equação:

As soluções são:

Considerações Finais

Resolver equações do 2º grau é uma habilidade essencial no estudo da matemática. A fórmula de Bhaskara é uma ferramenta indispensável para lidar com as equações completas, enquanto as equações incompletas podem ser resolvidas de maneira mais direta. A prática com exemplos e exercícios fortalece essa compreensão, permitindo enfrentar problemas mais complexos no futuro.

Por fim, lembre-se que a análise do discriminante \\( \\Delta \\) oferece uma visão clara sobre o número de raízes reais de uma equação, simplificando a abordagem ao problema.